What is the problem of radiation-reaction?
The shortest way to describe the problem of radiation-reaction is as follows: if an accelerating charge loses energy by emitting radiation, how does this energy loss affect the charge itself?
Now let's get a bit technical.
The equation of motion for an electron with charge 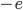 and mass
and mass 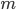 in an external electromagnetic field is given by the Lorentz force equation
in an external electromagnetic field is given by the Lorentz force equation
where 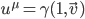 is the four-velocity of the electron,
is the four-velocity of the electron, 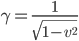 ,
, 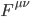 is the electromagnetic tensor and the dot represents differentiation with respect to proper time
is the electromagnetic tensor and the dot represents differentiation with respect to proper time 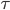 . Here I use the metric convention
. Here I use the metric convention 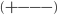 and units in which the speed of light is unity
and units in which the speed of light is unity 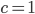 . According to Maxwell's theory of electromagnetism, the rate at which energy is emitted from the charge with respect to laboratory time is given by the relativistic Larmor formula
. According to Maxwell's theory of electromagnetism, the rate at which energy is emitted from the charge with respect to laboratory time is given by the relativistic Larmor formula
This radiation emission rate  is a positive-definite Lorentz invariant, which vanishes if and only if
is a positive-definite Lorentz invariant, which vanishes if and only if 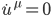 . This means that a charge emits radiation relative to a Lorentz observer if and only if it is being accelerated. The emission of energy in the form of radiation should result in energy loss by the charge, and consequently in a change in the dynamics of the charge. This modified dynamics is not present in the Lorentz force Eq. (1).
. This means that a charge emits radiation relative to a Lorentz observer if and only if it is being accelerated. The emission of energy in the form of radiation should result in energy loss by the charge, and consequently in a change in the dynamics of the charge. This modified dynamics is not present in the Lorentz force Eq. (1).
Heuristically, one can think of the radiation emitted from the charge like a bullet shot from a gun. When a bullet is shot from a gun, the bullet exerts a recoil force on the gun (in the opposite direction to the bullet's velocity). Similarly, the radiation emitted by the charge is expected to exert a recoil force on the charge, acting in addition to the usual Lorentz force. In this case it is a bit more tricky in terms of the direction of the force, but I'll discuss such subtleties later on. The upshot is that if the Lorentz force Eq. (1) doesn't account for the radiation-reaction force, it is only an approximated equation of motion, which is therefore limited to cases in which the radiation emission is small.
This is how most physicists think of the radiation-reaction problem, as an issue with the Lorentz force Eq. (1). However, before we jump to conclusions we should note that this is only one way to think of this problem. There are many others, as the problem may be more fundamental than this. Since the problem of radiation-reaction floats to the surface when considering radiation via the Larmor formula (2), which in turn, originates in Maxwell's equations, there might be something wrong with Maxwell's equations themselves. Nevertheless, because we don't know how to solve this problem it is very difficult to pinpoint where the exact issue is. I'll try to be brave and do it later on in this manuscript. Either way, the problem of radiation-reaction is a problem with the Maxwell-Lorentz theory of electromagnetism (and not necessarily only with Maxwell's equations or only with the Lorentz Force Eq. (1)).
One thing that is very exciting about the problem of radiation-reaction, is that it belongs to a very interesting (in my opinion the most interesting) class of problems. Thomas Kuhn divided the scientific endeavor into three phases:
- 'Pre-paradigm phase': in which there is no consensus on any particular theory, and many incomplete theories are available. When a consensus forms, the scientific community migrates to the second phase.
- 'Normal science': this is what we do most of the time. We take problems that can be formulated via the current paradigm and we solve them using the same paradigm (the current paradigm is the standard theory we use in a given field. For example in gravitational theory, general relativity is the current paradigm, while in particle physics it is the standard model). As long as there is consensus within the discipline, normal science continues. However, eventually enough progress in normal science reveals anomalies - these are facts that cannot be explained with the current paradigm. In most cases, such anomalies are resolved within the paradigm. But in some cases they may accumulate to the point where the scientific community is unsatisfied with the paradigm. Kuhn refers to this as a crisis. After a crisis, the third phase begins.
- 'Revolutionary science': this is the most exciting phase. It is the phase when the underlying assumptions of a field are reexamined and a new paradigm is established. Once this new paradigm is accepted, normal science restarts.
So how is this related to the problem of radiation-reaction? Well, the problem of radiation-reaction definitely does not belong to the kind of problems solved from within the paradigm itself. The problem of radiation-reaction is a fundamental issue with the Maxwell-Lorentz theory of electromagnetism. Since the problem involves the building blocks of the theory (the equations the entire theory is based upon), it cannot be solved using the Maxwell-Lorentz theory. A solution of the radiation-reaction problem would mean replacing the Maxwell-Lorentz theory of electromagnetism. This is one reason that I think the problem is very exciting.
"But isn't the problem of radiation-reaction resolved within quantum theory?" - is a question I often receive. Later on I'll prove that the answer to this question is a sounding NO. The problem of radiation-reaction is still unsolved in the framework of quantum theory. This has striking consequences, as it means that a solution of the radiation-reaction problem means a phase of revolutionary science that is going to be very revolutionary. The theory of matter as we know it will have to be revised to some extent, and the consequences of such a change might affect problems like dark energy, dark matter and many other fundamental things we fail to understand. This are not mere speculations, later on I'll try to provide some reasons to believe this is the case. For now, I'll just remind the reader that a synonym for the problem of radiation-reaction is "the self-force problem", which originates in our notion of matter.
During the development of the Lorentz-Maxwell formulation of electromagnetic theory there has been a long search for an improved classical equation of motion that comprehensively describes the dynamics of a radiating charge. This search is the topic of the next sections. Later on I will explain other attempts to solve this problem like the Born-Infeld theory. After this, we will touch the most subtle point of why this problem remains unsolved in quantum theory.






